Stumper is a word game that I came up with on a long train ride to Tokyo. My wife and I were starving and needed a distraction - Stumper was the best I could manage.

The rules are simple - start with a random four letter word and perform one of the following move types:

• Anagram - make an anagram of the word (eg. STAR -> (ARTS))
• Alteration - edit a single character of the word (eg. STAR -> S(O)AR)
• Addition - extend the word by inserting a single character (eg. STAR -> S(I)TAR)

Then, use your new word as your starting point and repeat the process until you either run out of moves or reach a word from which none are possible (a “Stumper”).

You start with only three moves. Anagrams and Alterations decrease your move count by one. You gain moves by playing Additions, which increase your move count by two. Words you play must be unique (no repeats) and valid according to the English Scrabble dictionary.

Each valid move gains points equal to the length of the word you’re changing, so each of the three example moves above would be worth four points (STAR is four letters long). The objective is to earn as many points as possible before the game ends.

You can play Stumper in your head, with a pen and paper, or online here.

Earlier this week, a friend nerd sniped me into figuring out an optimal pattern of play for Stumper. Against my better judgement, I set off on a journey to write a solver for the game.

If you’d like to take a crack at writing your own solver (or want to try playing the game without any hints), stop reading now and come back later :)

High-Level Problem

At its core, Stumper is a graph problem. We can model the game state as a graph with words as nodes and weighted edges between them representing possible moves and their respective scores.

For any given starting node, we want to find the highest scoring path without running out of moves at any point. We also need to be careful not to repeat any nodes, as that would violate the unique word rule. This is a variant of the NP-Hard longest path problem, so we can be pretty confident that we’ll need to do better than brute force here.

My goal was to write something that could run on my personal computer and find a solution for all 4030 valid Stumper starting words in a reasonable amount of time. I was able to achieve these goals with a small rust program that runs in just under 30min on my 6 core / 12 thread 3.7GHz machine. For comparison, I also wrote a brute force solver that checks every possible sequence of play for a given start node. I let it run for 10 hours before killing it, at which point it had only made it through 0.15% of all possible games.

A Tiered Solution

Starting out, I felt that I needed a way to cache and reuse results. With an acyclic graph, we could cache the optimal path from each node when we first explore it, then reuse that result every subsequent time we reach that node. The presence of cycles makes this much harder though, because the optimal path from a node is dependent not just on the node itself, but also on the path taken to get there (as we are not allowed to visit nodes more than once).

In the general longest path problem, there’s no way around this issue. In the context of Stumper, though, there’s one crucial rule we can exploit that allows us to cache some of our work.

If you recall the three move types, both the Anagram and Alteration move types are reversible. For any two word nodes A and B, if an edge A -> B exists due to an Anagram or Alteration move, there must also exist an edge from B -> A. The Addition move is the opposite. Because there are no word shortening moves in Stumper, if an edge A -> B exists due to an Addition move, it is guaranteed that B -> A does not exist. In fact, from a node with a given word length, it is guaranteed that no paths exist to any node with a shorter word length. Once you play a word with length seven, you can’t play a word of length six, five, four, etc.

With this in mind, we can split the graph into “tiers” based on node word length. Between each of these tiers there exist only edges going in one direction - from the lower tier to the higher tier. This creates a sort of barrier across which cycles cannot form, and is the key my solution.

As stated before, our main obstacle to caching results is the fact that we need to remember which nodes we’ve visited and avoid creating cycles. Whenever we enter a tier for the first time, though, it is guaranteed that all previous moves happened on lower tiers - tiers that we are guaranteed to never be able to access again. As such, each of these tier “entry points” acts as a clean slate. Whenever we enter a tier through one of these entry points, it will always have the same optimal path going forward, regardless of the path we took to get there.

To solve the whole graph, we can just go through our tiers from highest to lowest, run exhaustive search for each possible entry point into the tier, and cache that result. Then, whenever we encounter a higher tier node on our path, we can perform a cache lookup for its optimal score and avoid performing duplicate work. Here’s the core outer loop of the algorithm in python:

cached_optimums = {}

for tier in tiers.descending_wordlength_order():
    # Whether or not a node is a valid entry point is precomputed
    # when we generate the graph
    for entry_node in tier.entry_nodes:
        # The max possible moves we could have left when reaching a node
        # is also precomputed during graph generation
        for moves_remaining in range(0, entry_node.max_moves + 1):
            optimal_score = solve_node(entry_node, moves_remaining, set())

            cache_key = (entry_node, moves_remaining)
            cached_optimums[cache_key] = optimal_score

Note the presence of moves_remaining above. I have avoided discussing it up to this point for simplicity’s sake, but it is very important. Because of the move gain/loss mechanics in Stumper, the optimal solution for any given entry point is dependent on the number of moves we have left upon reaching the node. We therefore need to perform our exhaustive search and update the cache for every possible combination of entry_node and moves_remaining.

Here’s an implementation of solve_node:

def solve_node(node, moves_remaining, visited):
    if moves_remaining == 0:
        return 0

    visited.insert(node)

    optimal_score = 0
    for child in node.children:
        if child in visited:
            continue

        # If this is an Addition, gain moves and check our cache
        if child.word_length > node.word_length:
            cache_key = (child, moves_remaining + 2)
            child_score = cached_optimums[cache_key]
        # Otherwise, call the recursive case with one fewer move
        else:
            child_score = solve_node(child, moves_remaining - 1, visited)

        if child_score > optimal_score:
            optimal_score = child_score

    visited.remove(node)

    # In Stumper, each move is worth a number of points
    # equal to the length of the current word.
    return optimal_score + node.word_length

When our algorithm is done running, we can get the answer for any given starting word by checking the cache entry for (starting_node, 3) (starting move count is three).

Note that we haven’t actually found a way to avoid solving the longest path problem - we’re still enumerating every possible path within each tier. The major speedup accomplished by this solution comes from eliminating any cross-tier paths and the drastic reduction in search space that provides.

Analysis

After letting my solver run to completion, I started to look for patterns in the paths. It immediately became clear that optimal play is highly homogeneous. Out of all possible games, 99.4% (4005 out of 4030) of them end with either FORMALITIES, ORIENTALISTS, or PHRENOLOGIES. The rest of the games are almost entirely 1-2 move dead ends, except for a cluster of three starting words (OUZO, QUEY, and KUDO) that play a full game and end on REELECTIONS.

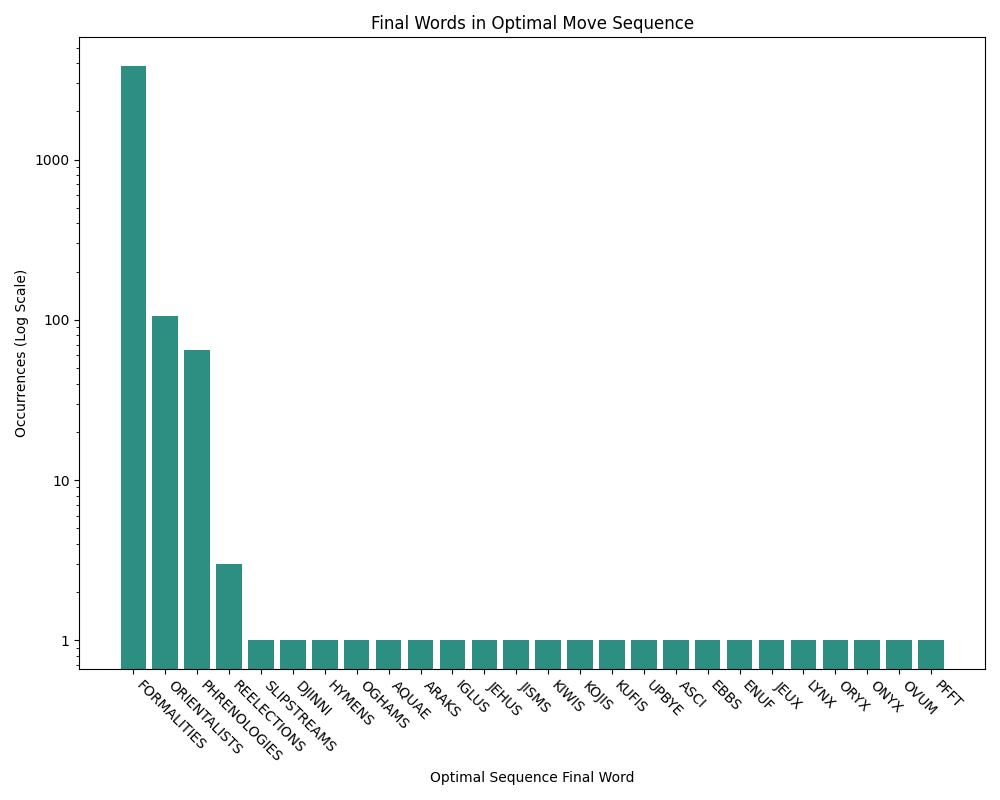
The optimal strategy is essentially to speedrun from your starting word to a long, high scoring subsequence that leads up to one of these final words. Most of them look something like Starting Word -> ... -> LIGATIONS -> LIBATIONS -> LIBRATIONS -> LIBERATIONS -> LITERATIONS -> ORIENTALIST -> ORIENTALISM -> ELIMINATORS -> NORMALITIES -> FORMALITIES.

Looking at this, you can see that things are even more homogenous than they initially appeared. It turns out that ORIENTALIS* is actually just a stepping stone to FORMALITIES, so games ending with ORIENTALISTS are really just attempts to get to FORMALITIES that run out of moves.

It’s worth noting that the algorithm will keep using the same optimal path subset once it has found one, even if there are paths that would give equivalent scores. Because of this, there may actually be multiple unique ways to reach the same (but not a higher) optimal score that are not showcased in the results. I did rerun the solver once with a shuffled exploration ordering to see if it would drastically change the results. There were some changes to early game word selection, but the mid and endgame paths stayed the same. My gut tells me that these optimal final words we’re seeing are actually unique global optimums, but I’d need to tweak the algorithm slightly to actually verify that.

Games ending in PHRENOLOGIES are the highest scoring games possible, and include starting words such as LAGS, TORY, PONY, etc. These words are valuable because they can easily be transformed into the highest scoring starting word in the game - LOGY with an optimal score of 247. The LOGY path goes through various -logies like HEMOLOGIES, VENOLOGIES, NEPHOLOGIES, etc. before finally ending on PIGEONHOLES -> PIGEONHOLED -> PIGEONHOLER -> PIGEONHOLERS -> NEPHROLOGIES -> PHRENOLOGIES. You can see this in the optimal score distribution below, where the small cluster around 250 is the PHRENOLOGIES path and the larger one around 200 is the ORIENTALISTS / FORMALITIES path.

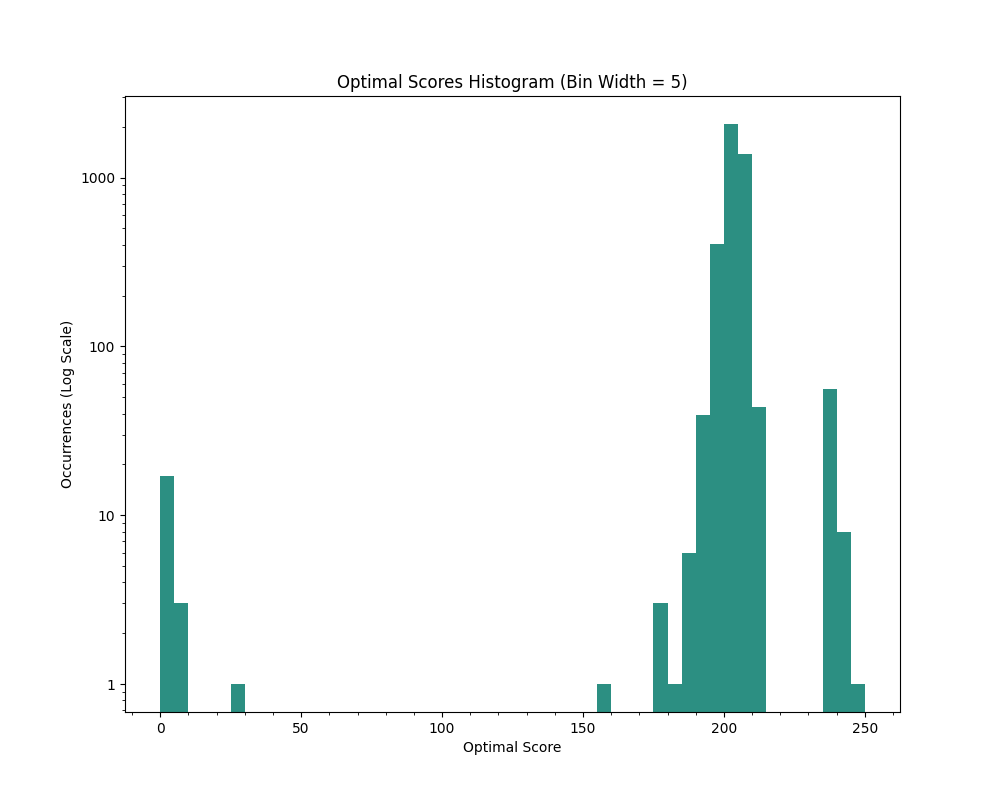
For reference, the best scores that I’ve seen come out of a human are in the ~100-110 range.

Impact on Human Play

So how might this inform human strategies? To help answer this, I put together a flowchart that shows many common paths taken to FORMALITIES, ORIENTALISTS, and PHRENOLOGIES. Each node shows the number of times a word occurs in an optimal path (out of 4030 possible games). Each edge indicates that a move between the connected words is played in at least one optimal path. The chart is not exhaustive, but does capture most words that occur more than ~50 or so times in optimal paths. You can click the link below to view it at full scale. However, I’d encourage you to play a few rounds for yourself before looking.

Click here to view the full-res flowchart.

When I first saw this chart, I was a little disheartened. It seemed trivial to memorize some of these common sequences and just play words until you get to one of them. After trying to play like that, though, I still find the game quite challenging. For many words it can be surprisingly hard to get onto one of these sequences - even with this cheat sheet open. It’s also not always obvious which entry point or subsequence you should even be aiming for. On top of that, you still need to manage your remaining move count and figure out when to spend your moves on the current tier vs. moving up the tiers.

Conclusion

To be honest, I like the game a lot more when playing unburdened by the weight of “optimal” play. In my opinion, it’s much more fun to react to the words you’re given rather than relying on memorization. I think that an interesting variant of Stumper would be one where you try to find the shortest path between a random starting and ending word, rather than trying to get a high score. It would be much easier to solve for a computer, but it might make it harder for a human to fall back on rote memorization of subsequences.

You can find the source code for the actual rust solver here. That repo also contains some python utilities for generating / querying the word graph, as well as the source for the web version of the game.

If you’d like to perform your own analysis / create your own visualizations of the results, JSON output of the optimal solutions to all starting words can be found here.

If you’ve made it to this point and want another challenge, try solving the two-player variant of the game. The core rules are the same, but two players alternate making moves on a single word. There’s no score, the winner is just the last player standing who makes a valid move. You can try this variant of the game in the web version by going into the menu and clicking on “Versus Mode”. I’d imagine this version is actually easier to solve, but I don’t know that for sure.